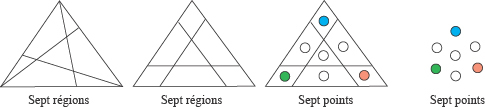
À l’intérieur d’un triangle, traçons trois segments joignant chacun un sommet au côté opposé. On obtient ainsi au maximum sept régions intérieures au triangle, à condition que les trois droites ne soient pas concourantes.

Si l’on trace des segments parallèles aux côtés du triangle, on aboutit également, au maximum, à sept régions.

Plaçons des points à l’intérieur des sept régions, puis effaçons le tracé du triangle et des segments. Les sept points peuvent alors être regroupés pour former un hexagone centré.

En faisant la même expérience avec trois fois deux segments à l’intérieur du triangle, on obtient dix-neuf régions et dix-neuf points, que l’on peut regrouper pour former le troisième nombre hexagonal centré, c’est-à-dire 19 (les deux premiers étant 1 et 7).

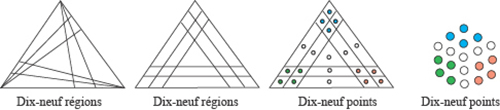
1. Combien obtiendrait-on de régions et de points en traçant trois fois trois segments à l’intérieur du triangle ? Et en traçant trois fois n segments ?

Différences de cubes consécutifs

Une autre situation permet de retrouver ces nombres hexagonaux centrés. Traçons un triangle, puis deux triangles superposés, puis trois… On retrouve ces mêmes nombres hexagonaux centrés avec les nombres maximaux de régions fermées délimitées par ces tracés de triangles.

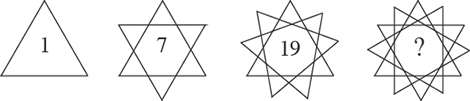
Plus étonnant : les nombres figurés trouvés, à savoir 1, 7, 19…, peuvent également être obtenus comme différences de cubes d’entiers consécutifs. En effet :

1 = 1³ – 0³ ;

7 = 2³ – 1³ ;

19 = 3³ – 2³ ; et ainsi de suite.

2. Démontrez que le n^ième nombre hexagonal centré est égal à la différence de deux cubes d’entiers consécutifs.