Les nombres de Queneau

Le troubadour français Arnaut Daniel (1150‒1210) est donné pour être l’inventeur de la sextine. Dante (1265‒1321) et Pétrarque (1304‒1374) ont eux aussi composé des sextines. Cette forme continue à être utilisée par les poètes contemporains pour créer, dans toutes les langues, des textes riches en musicalité et en sens.

La sextine se compose de six strophes de six vers, suivies de l’envoi, généralement composé de trois vers (tercet). Les six mots finaux de chaque vers de la première strophe sont ensuite réorganisés dans les strophes suivantes, de sorte que chaque mot final soit utilisé une fois par strophe, en fin de vers, mais dans une position différente à chaque fois. L’envoi reprend les six mots finaux.

La permutation qui permet de définir l’ordre des mots finaux d’une strophe à partir de ceux de la strophe précédente est la suivante :

1   2   3   4   5   6

6   1   5   2   4   3

De la sextine à la quenine

Cette permutation permet de terminer le premier vers d’une strophe par le même mot que celui qui termine le dernier vers de la strophe précédente, produisant ainsi un effet de répétition.

La structure élaborée de la sextine, avec sa répétition de mots finaux, crée un effet de circularité et de variation tout au long du poème. Cela nécessite un travail méticuleux pour choisir les mots finaux appropriés et les intégrer harmonieusement dans chaque strophe ! Composer une sextine est un défi pour les poètes en raison de sa structure contraignante, mais elle permet également une exploration créative et une maîtrise formelle. Il n’est donc pas étonnant que le cofondateur de l’Ouvroir de littérature potentielle (Oulipo), Raymond Queneau, étudie cette forme contrainte, jusqu’à en théoriser une généralisation. Il inventera pour cela la quenine, ou n-ine, famille de formes poétiques de n vers basée sur une permutation de Queneau‒Daniel d’ordre n. Si n est un entier, la permutation est définie par :

On retrouve la sextine avec la quenine d’ordre 6 :

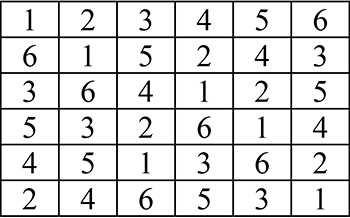
Après application de la permutation, tous les chiffres occupent bien une position différente. De plus, une septième permutation ramènerait à la configuration initiale.

La « quenine d’ordre 4 » est impossible car l’un des chiffres (en rouge) reste invariant :

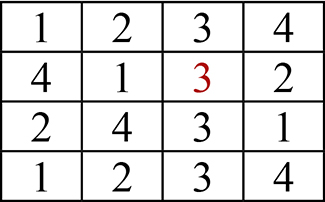
On dit que n est un nombre de Queneau si, et seulement si, il existe une quenine d’ordre n. Les premiers termes de la suite fondamentale de Queneau sont :

1 (unine ou monine), 2 (didine), 3 (terine), 5, 6, 9, 11, 14, 18, 23, 26, 29, 30, 33, 35, 39, 41, 50, 51, 65, 69, 81, 86, 90, 95, 98, 99.

Une 99-ine est un poème de neuf mille huit cent un vers, sans compter l’envoi !

Un critère, issu de la théorie des groupes, permet de caractériser les nombres de Queneau. En considérant le groupe G des éléments inversibles du groupe  , un entier n est un nombre de Queneau si, et seulement si, deux conditions sont remplies :

1) 2n + 1 est premier ;

2) soit 2 est d’ordre 2n dans G, soit n est impair et 2 est d’ordre n dans G.

On conjecture qu’il existe une infinité de nombres de Queneau, toujours sans preuve à ce jour !