Une extrapolation qui tient la corde
Notre intuition est ô combien faillible. Dans notre quotidien, nous sommes, hélas, irrémédiablement irrationnels. Voici quelques exemples où notre raison, à savoir notre capacité d'extrapolation et de prédiction, échoue malgré tout. Les choses parfois sont simplement plus compliquées qu'elles n'en ont l'air, surtout dans le monde des maths !
Dans ce petit problème, il s'agit de diviser un cercle en régions avec des cordes. Plaçons donc des points sur la circonférence d'un cercle et traçons toutes les cordes possibles passant par ces points en les reliant deux à deux. Le but est de deviner le nombre de régions p créées par n points. Comme illustré ci-dessous, les réponses pour n = 1, 2, 3, 4 et 5 sont respectivement p = 1, 2, 4, 8 et 16.
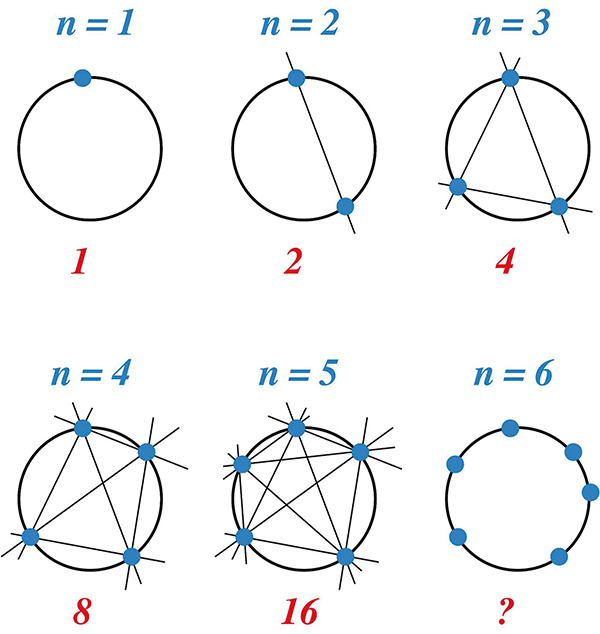
Pouvez-vous trouver la valeur suivante ?
Par induction, il semble légitime de penser que le nombre de régions p est lié à la formule 2n–1, et donc de conclure que la sixième valeur est 32. Que nenni ! En réalité, la réponse est 31, et la formule pour trouver la énième valeur de p est en fait un peu plus sophistiquée :
p = (n 4 – 6n 3 + 23n 2 – 18n + 24) / 24.
Indomptables nombres entiers
Au XVIIIe siècle, Leonhard Euler (1707-1783) exhibe un étonnant polynôme du second degré, n 2 + n + 41, qui possède la remarquable propriété de produire un nombre premier pour n = 0, pour n = 1, pour n = 2… et pour n = 39. Rien que ça ! On serait tentés d'en déduire que ce polynôme ne fournit que des nombres premiers. On commettrait alors une belle erreur ! En effet, pour n = 41, le polynôme fournit clairement un grand multiple de 41, et la magie s'envole. On appelle depuis nombre chanceux d'Euler un entier c > 1 tel que n 2 + n + c est un nombre premier pour tout n allant de 1 à c – 2. En 1952, il a été prouvé que les seuls nombres chanceux d'Euler sont 2, 3, 5, 11, 17, 41.
Quittons les nombres premiers. L'égalité en nombres entiers x 4 + y 4 + z 4 = w4 traduit quant à elle une équation diophantienne dont le grand Euler, toujours lui, avait cru qu'elle n'admettait aucune solution en nombres entiers. Pendant deux cents ans, personne ne put prouver la conjecture d'Euler, ni la réfuter par un contre-exemple valide. Puis, un jour, en 1988, Noam Elkies de l'Université de Harvard (Massachusetts, États-Unis) a découvert à l'aide de mathématiques sophistiquées et d'une grosse puissance de calcul la solution suivante :
2 682 4404 + 15 365 6394 + 18 796 7604 = 20 615 6734,
prouvant qu'il existait bel et bien un solution positive. Ainsi, Euler s'était trompé… Pire encore : Elkies a prouvé qu'il y avait une infinité de solutions à l'équation de départ ! Par la suite, Roger Frye trouva même le plus petit contre-exemple possible en utilisant un ordinateur et les conseils d'Elkies :
95 0004 + 217 5194 + 414 5604 = 422 4814.
Des carrés qui ne tournent pas rond
Regardez cette magnifique formule bien dans les yeux :
N = 991n 2 + 1.
Si vous vous amusez avec (à l'aide d'un outil de calcul formel par exemple), vous vous convaincrez peut-être que N ne peut jamais être un carré parfait, quelle que soit l'entier n. Jusqu'à un million, ça marche, on ne trouve aucun N qui soit un carré parfait. Jusqu'à un milliard, ça marche aussi. Jusqu'à un milliard de milliards, ça marche toujours. Mais alors, la formule serait-elle correcte ? Eh bien non, car :
991 × 12 055 735 790 331 359 447 442 538 7672 + 1 = 379 516 400 906 811 930 638 014 896 0802.

