Le système Chaldéen

Au début du XIII^e siècle, l'archidiacre Jean de Basingstoke a introduit une notation pour représenter les nombres compris entre 1 et 99 sur la base d'un trait vertical muni d'un appendice à gauche (représentant des unités) et d’un autre à droite (dizaines). Plusieurs variantes de ce système se retrouvent dans divers manuscrits cisterciens, et ont été utilisés dans une variété de buts, en concomitance avec les chiffres romains et indo-arabes. Ce système numérique original appelé alors « Chaldéen » est tombé petit à petit en désuétude et a été oublié.

Le système d’Agrippa

Un système de notation numérique analogue dit « Notae Elegantissimae » d'Agrippa (voir ci-dessous) permet d'écrire des nombres de 1 à 9999, sa compacité fit qu’il fut principalement utilisé à des fins d'indexation.

Mais il est également utile comme aide mnémonique. Par exemple, le symbole ‘K’ dans l’exemple ci-dessous peut signifier 1414 (les 4 premières chiffres de la racine carrée de 2).

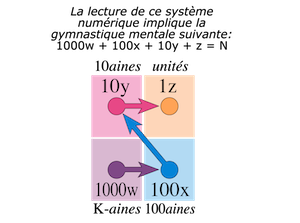
La lecture se pratique dans l’ordre suivant :

• en bas à gauche pour les milliers,
• en bas à droite pour les centaines,
• en haut à gauche pour les dizaines,
• en haut à droite pour les unités.

Le système Katapayadi

Le système Katapayadi est une ancienne notation numérique qui représente les chiffres par des lettres (l’écriture indienne est syllabique !). Chaque chiffre ayant plus d’une valeur syllabique, cela permettait de former des mots significatifs et des versets poétiques à partir de n’importe quel nombre :

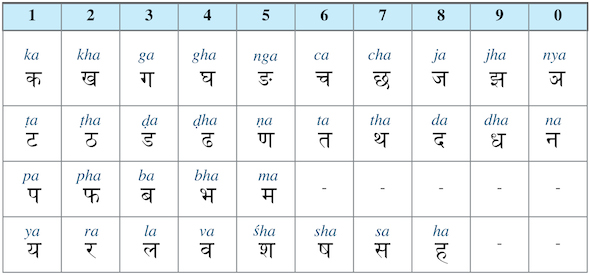
C’est donc un système mnémonique puissant, qui était également utilisé pour crypter des formules mathématiques. Par exemple, le verset suivant du VII^e siècle est une invocation à Shiva, qui donne la valeur de Pi jusqu’à la 31 décimale ! Le lecteur est invité à le décrypter en s’aidant de la table…

Un système corporel à base 27

Le peuple Oksapmin de la Nouvelle-Guinée dispose d'un système de numération à base 27. Lors de comptages, chaque nombre porte le nom d’une des 27 parties du corps, en commençant par le pouce de la main droite, allant jusqu'au nez, puis descendant vers la partie opposée du corps jusqu’au petit doigt de la main, comme indiqué dans le dessin.

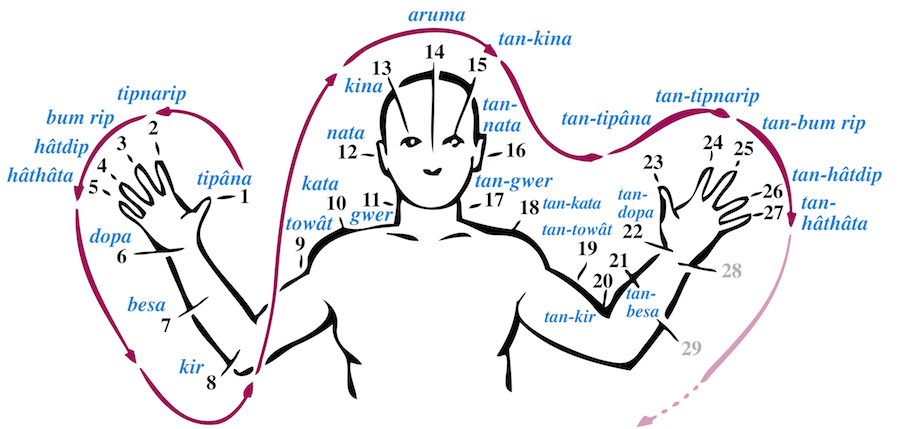
Un se dit ‘tipâna’ (pouce), 6 est ‘dopa’ (poignet), 12 est ‘nata’ (oreille), 16 est ‘tan-nata’ (oreille de l'autre côté), et pour finir 27, ‘tan-hâthâta’ (petit doigt de l'autre côté). La direction du comptage est parfois arbitraire et est plutôt liée à la gestuelle… En général, les Oksapmins comptent à voix haute en montrant la partie du corps qui représente le nombre concerné et, lorsqu’ils dépassent le nombre 27, ils ont coutume de crier « fou ! », qui signifie ‘complet’ et de soulever les poings. Le mot « fou » qui représentait 27 ou un ‘grand nombre’ s’est par la suite adapté à notre système décimal et signifie désormais ‘vingt’.

S’ils doivent compter au-delà de la 27ème partie du corps, les Oksapmins inversent la direction de comptage et repartent en boucle à partir du poignet, soit ‘dopa’ (28), etc.

Dans la vidéo, bien que la femme énumère les nombres de façon appropriée, elle a sauté par inadvertance le nombre 18, soit « tan-kata » qui signifie ‘épaule opposée’.